90% vs. 95% confidence interval: which to use?

Ever wondered how statisticians estimate the unknown with such confidence? One of their go-to tools is the confidence interval—a method that provides a range of plausible values for an unknown parameter. Instead of offering just a single estimate, confidence intervals give you an interval that is likely to contain the true value, based on a chosen level of confidence.

In this blog, we'll break down what confidence intervals are, explore the difference between 90% and 95% confidence levels, and discuss how to choose the right one for your analysis. We’ll also look at real-world applications and the factors that influence your choice. Let’s dive in!

What are confidence intervals?

A confidence interval is a range of values, derived from sample data, that is used to estimate an unknown population parameter, such as a mean, proportion, or difference between groups. Instead of relying on a single point estimate (like a sample average), a confidence interval provides a range of plausible values where the true value is likely to fall. This approach accounts for sampling variability and helps express the uncertainty that naturally comes with working from a sample rather than an entire population.

Every confidence interval comes with a confidence level, typically expressed as a percentage—commonly 90% or 95%. This number reflects the long-run success rate of the method: if we were to take many samples and compute a confidence interval from each, about 95% of those intervals (for a 95% CI) would contain the true population parameter. Importantly, the confidence level does not mean there’s a 95% chance that the specific interval you computed contains the true value. Rather, it reflects how confident we are in the method over repeated sampling.

The width of a confidence interval reflects the precision of your estimate. A narrower interval means more precision, while a wider interval reflects greater uncertainty. Several factors influence this width:

1. Sample Size: Larger samples generally lead to narrower intervals, because they provide more information about the population.

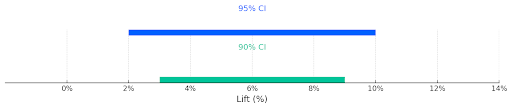
2. Confidence Level: Higher confidence levels (e.g., 95% vs. 90%) require wider intervals to ensure the parameter is captured more reliably.

3. Variability in the Data: More variability in the sample increases the width of the interval, as the estimate is less stable.

4. Standard Error: Confidence intervals are built using the standard error of the estimate. Anything that reduces standard error (like increasing sample size or reducing variability) will tighten the interval.

Typically, the main way analysts can influence the width of a confidence interval—and thus its precision—is by adjusting the sample size. However, in many real-world scenarios, particularly in industry, analysts also have some flexibility in choosing the confidence level, which directly affects the interval’s width. In the next section, we’ll discuss how to determine the appropriate confidence level for your analysis. While 95% is the standard in academic research, 90% is also commonly used in industry settings. Ultimately, the right choice depends on the context, the potential consequences of incorrect conclusions, and the level of uncertainty you’re willing to tolerate.

Understanding the difference between 90% and 95% confidence levels

At the end of the day, picking between a 90% and 95% confidence level depends on what you're trying to achieve. As Statsig's blog post on the 95% confidence interval suggests, you might need to adjust the standard 95% level based on your unique risk profiles or statistical power needs.

To choose between a 90% and 95% confidence level, it’s important to understand how confidence level affects risk tolerance and precision—two factors that often trade off against each other. A lower tolerance for risk calls for a higher confidence level, which results in a wider interval to reduce the chance of error. However, this wider interval comes at the cost of precision. Conversely, if you prioritize high precision, you’ll need to accept a slightly higher level of risk in exchange for a narrower confidence interval—gaining precision but increasing the likelihood of error.

When evaluating these factors in your decision of confidence level, two key factors should be considered. First, what is the potential cost of making an error? In the digital industry, launching a neutral or non-improving feature often has minimal consequences, making a 90% confidence interval a reasonable and efficient choice. However, in high-stakes fields like medicine, the cost of error is significantly greater—approving an ineffective treatment can waste resources, delay better options, or even harm patients. In such cases, a more cautious and risk-averse approach is warranted, typically favoring a 95% confidence interval to reduce the likelihood of false positives.

Second, it’s important to understand the implications of changing the confidence level. Lowering it from 95% to 90% effectively doubles the false positive rate—that is, the chance of detecting a significant effect when none actually exists. While this trade-off might seem acceptable at first glance, the impact can be substantial. False positives may account for a large share of all statistically significant results, which over time can erode trust in data and undermine decision-making.

For example, if the true improvement rate is around 10% and the test has 80% power, using a 95% confidence level results in about one-third of significant findings being false positives. Reducing the confidence level to 90% raises that proportion to nearly half. This means that about half of the changes implemented based on "significant" results will actually yield no real improvement—potentially leading to wasted resources, poor product decisions, and growing skepticism toward experimentation as a whole.

Keep in mind that confidence intervals often go hand in hand with hypothesis testing, as both provide insights into the reliability of an estimate. In two-sided tests, there's a direct connection between CIs and p-values: if a 95% CI does not include the null value (e.g., zero for a difference), the corresponding p-value will be below 0.05, indicating statistical significance. Conversely, if the CI includes the null, the result is not significant at that level. Therefore, choosing between a 90% and 95% confidence level also affects the outcome of the hypothesis test—lowering the confidence level can make it easier to reject the null hypothesis, but at the cost of increased risk of Type I error.

Finally, the choice between a 90% and 95% confidence level often depends on available resources. Specifically, a 90% confidence level requires a smaller sample size than 95%, making it a practical option when sample sizes are limited. This helps keep the test manageable and reduces its duration—an important advantage for companies or situations where collecting large samples is challenging.

Practical applications of selecting confidence intervals in analysis

Choosing the right confidence level depends on the context and the goals of your analysis. For high-stakes decisions, a 95% confidence interval is often preferred because it reduces the risk of false positives, offering greater certainty—though at the cost of wider intervals and lower precision. In contrast, for exploratory research or early-stage experiments, a 90% confidence interval may be more appropriate. It allows for quicker detection of potential trends or effects and can be especially useful when sample size is limited, even though it comes with a slightly higher risk of Type I errors.

It's also important to note that adjusting the confidence level isn’t the only way to influence the width of an interval. While increasing the sample size is one option, it’s not always feasible—especially when dealing with low-count data or imbalanced groups. In such cases, Bayesian methods like empirical Bayes estimation can offer an alternative. By incorporating prior information, these approaches shrink individual estimates toward the overall mean, improving reliability and stability. This is particularly useful in fields like genetics and advertising. From these methods, credible intervals—the Bayesian equivalent of confidence intervals—can be constructed. These intervals often provide narrower, more informative ranges when data is limited.

Closing thoughts

Confidence intervals are more than just numbers—they're essential tools for understanding the uncertainty around your estimates. The choice between a 90% and 95% confidence interval ultimately depends on the context of your analysis. Ask yourself: What are the consequences of being wrong? How large is your sample? And how much precision do you need? By weighing these factors, you can select a confidence level that balances risk, precision, and feasibility.

Importantly, the confidence level should be chosen before collecting data to ensure consistency and avoid bias. Sticking to a pre-defined standard across similar experiments also improves the reliability of your conclusions. Consider your unique risk tolerance and statistical power requirements to determine the level that best fits your goals.

At Statsig, we understand how crucial it is to choose the right confidence level for your experiments. Our platform offers tools and resources to guide these decisions, helping you run better tests and draw more reliable insights. Check out our guides on confidence levels and intervals to deepen your understanding and improve the quality of your analyses.

Hope you found this useful!